
Online Bingo - Is It Fixed?

-
Updated: 23rd Jun 2025
Online bingo in the UK is heavily regulated by the Gambling Commission and UK bingo sites are amongst the most reputable in the world. Sites such as Mecca Bingo, Paddy Power Bingo and Unibet have won at industry events such as the EGR Operator Awards for social responsibility and fair play. Despite this many players apparently harbour a suspicion that all is not as it should be and in fact this is a major driver for players seeking out new bingo sites to play at in the hope of winning more often. So is it possible that online bingo games could be rigged?
- Common bingo complaints
- The heavy depositor effect
- Winning strategies?
- Statistics and bingo
- Do the numbers matter?
- Card selection ideas
- How many cards should you buy?
- Return To Player
- It’s all about the entertainment value
Common bingo complaints
Taking a look round a few forums reveals that when someone isn’t happy with an online bingo site, it’s generally for one of three reasons:
- Banned for playing excessive free bingo
- Something connected with withdrawal rules or wagering requirements.
- A belief that the games are fixed. The games are almost always won by the same people, they say, and often they weren’t even in the bingo room at the time!
While at times you may feel that there is an evil little creature looking over your shoulder, checking your card and quickly grabbing a number for the next call that isn’t on there, the truth is that bingo software uses a Random Number Generator and as long as you play at a site that is regulated in the UK, the RNG that they use will have to have undergone independent testing by a body such as eCOGRA or iTech Labs in order for them to gain their gaming licence. Many bingo sites have their RNG testing information available to view.
The heavy depositor effect
So why do the same names crop up as winners all the time? Well, the sad truth is that those players are almost certainly buying the maximum number of cards (often 96) for every single game, and pre-buying heavily when they can’t be around the computer – so while they are winning more often than you are, they are also depositing far more frequently and heavily than you are. And yes, in the extreme case that one of those players buys 96 cards for a game and you are the only other player and buy one card, they would be 96 times as likely to win as you – but if the site allowed such a game to run (which it probably wouldn’t due to too few players) the prize fund, if it wasn’t a guaranteed jackpot game, wouldn’t be enough to cover the cost of their cards (whereas if you did win, you’d clean up).
This heavy depositor effect is so widespread that the Gibraltar gambling regulator has actually published guidance about it on their “how to complain” page.
If you feel disadvantaged by other players buying so many tickets, many online bingo sites offer games where the maximum number of tickets allowed is low – Gala for instance have a room where the maximum purchase per game is 12 tickets and some forms of bingo designed for mobile and tablet play – such as Cash Cubes by Virtue Fusion – allow just one ticket per player and instead have a multi stake arrangement whereby players who buy in at a higher level are playing for a bigger prize.
The effect is confined to online bingo, of course. To play in a bingo hall one must be physically present and daub one’s own cards, so only a crazed insomniac octopus could manage to play 96 cards 24/7.
Winning strategies? – Granville’s Strategy & Tippett’s Strategy
But what are the chances of winning at bingo, and are there any strategies that can give you an edge?
Some sites have suggested that there are statistical theories which can give you an edge when selecting bingo cards. One of these theories is based on the work of the stock market pundit Joseph Granville who suggests avoiding “extreme” distributions when choosing cards, because, he says, balanced cards with an equal number of odd and even numbers and and equal number of high and low numbers are more likely to win. Granville wrote a book about it called How To Win at Bingo which currently seems to be out of print, but used copies are available on Amazon.
Another theory refers to the work of L.H.C. Tippett who was a respected statistician, though many of the pages that mention him seem to know so little about him that they spell his name incorrectly. The theory says that the more balls that are called in a bingo game, the closer the average of the balls that have been called so far gets to 38 in the case of 75 ball bingo and 45 in the case of 90 ball bingo – so you should choose a card with numbers that are close to the average in a 75 ball game you expect to be a long one (a complex pattern or coverall) and a card with numbers that are far from the average in a 75 ball game you expect to be a short one (a simple pattern) .
Statistics and bingo
To understand better why applying statistics to bingo can be misleading let’s look at what happens in a different scenario, one where we roll two 6 sided dice.
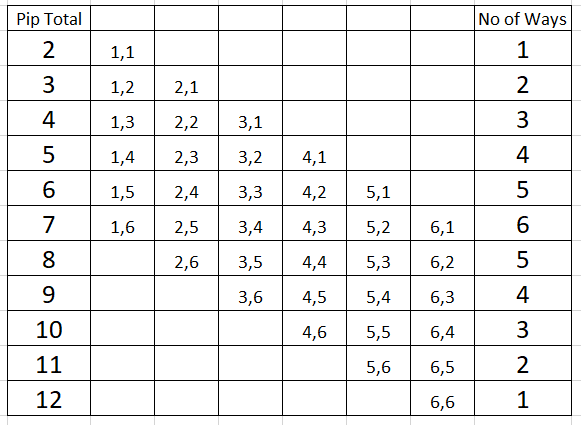
There are 36 different combinations, and the most common total is 7, with 6 different ways to score 7. Statistically, in a large number of random rolls of two dice, 7 would be the most common outcome (the mode), the middle value in the list if you put them all in ascending order would be 7 (the median) and also the average value of the sum of the pips would tend towards 7 (the mean).
Now, there are two ways of betting on this dice game. You can bet on the total of the dice, or you can bet on getting a specific combination. If you are betting on the total of the dice then that’s where statistics come into play. If you are betting on getting a specific combination, it’s very simple – assuming that the dice are not loaded the probability of getting any specific combination is 1/36, no matter what combination it is and no matter what the total of the pips on the dice is. Someone who observed this dice game many times would notice that there are more winners with the pip total of 7 than any other total.
Does this mean that if we are betting on a specific combination, it’s best to pick one of the combinations that add up to 7, such as green 3, orange 4? No it does not! While it is true that the 7-total combos win most often, that is because there are more of them – and we are only betting on one of them. There is a 1/6 chance that some 7-total combo will come up – and the chance of getting a specific one of those is 1/6 of that because there are 6 of them. 1/6 x 1/6 = 1/36 – which is the same chance as getting the snake-eyes .
Do you see now the problem with the Granville theory? It says that it’s more likely that the winner of a bingo game will be a balanced looking card – but that’s because, like the 7-total combos in the dice roll game, there are more balanced looking cards (out of the millions of possible bingo cards) than unbalanced looking cards. Since when you play bingo you are betting on a specific card – like picking a specific combination in the dice game – rather than on a type of card, that doesn’t make any difference to your chance of winning this particular game, which is still 1/n, where n is the total number of cards sold (a very small subset of the cards possible). If someone could take a look at all the cards that had been sold for the game (assuming they are randomly generated and allocated) they would notice that most of them were balanced looking.
We can play a simple form of bingo with this dice rolling game. We give each player a card with 3 combos on it, and roll the dice repeatedly until someone calls house. But this changes things, because applying any statistical analysis to the dice rolls becomes invalid; instead of looking at a large number of random rolls we are looking at a series of no more than 36 rolls where each combination is allowed once and once only.
That’s why Tippett’s work doesn’t apply to bingo calls – while it is true that the average of the balls called so far in a bingo game does tend closer to 38 or 45 the more balls are called, that is trivial – it is because there is one and only one ball with each number on so in the case that all are called, the average WILL be 38 (well, 37.5) or 45 and the more balls that have been called, the less effect the numerical value of the balls that are yet to be called will have on the total average. Same goes for the dice game – the average pip sum in 36 rolls where each combo is allowed once and once only WILL be 7. ANY attempt to correlate the balls called in a bingo game with any theories about statistical distributions is just plain wrong, because those theories apply to populations and events where each member of a population and each event has a value which does not depend on whether some other member of the population or some other event has already bagged that value! In THOSE sorts of distribution, outliers are rare – for instance, if the depth of a pond varies from 1 inch to 90 inches, the 1 inch and 90 inch events would be extreme and very rare, whereas there would be a lot of events in between 40 and 50 inches. In bingo on the other hand, ball 1 and ball 90 are each precisely as common as ball 45 (just like green 1, orange 1 being precisely as common as green 3, orange 4). The only way in which Tippett’s work has any relevance to bingo is in the random generation and allocation of the bingo cards – it tells us that bingo cards where the mean of the numbers that appear in a column is close to the median of the possible numbers that could appear in that column, are more commonly generated than cards where the two values are further apart (and guess what, that means that balanced looking cards are more common than unbalanced looking cards!).
Now, the probability of getting any specific combination is 1/(36-n) where n is the number of rolls that have already been made, and the probability of getting any pip total will depend on how many combos with that pip total, in that specific game, have already been crossed off the list. But remember that we are betting on combinations, not pip totals. The probability of a particular card winning does go up or down after the game starts depending on which combos have already been rolled and whether they were on the card – but since the cards have already been allocated before the game begins this does not help us with card selection (well, not without a time machine).
Do the numbers matter?
In fact, in the dice game where we are betting on a specific combo such as green 3, orange 4, the numbers on the dice are a red herring – replace them with letters or pictures and the situation becomes crystal clear as there’s no sum of the numbers to confuse the issue.
But what happens with bingo? Can the numbers be replaced with letters or pictures without changing the game? The answer is yes and no. Once the game has started and the numbers are being called, you can replace them with anything you like and it makes no difference – it’s still 90 or 75 unique items being pulled from a bag until someone matches all of them.
But where the numerical values DO come into play is in determining the (very large) set of possible legal bingo cards. Consider a 90 ball card with 1, 2 and 3 on it – it cannot also include any of the numbers from 4 to 9. Now consider a game where, as it happens, the balls 1, 2, 3 and 4 are first to be called. This sounds very unlikely (and it is) but in fact it is exactly as unlikely as any other specific combination of 4 balls – such as 1,11, 21 and 31. But there is already an asymmetry – in the 1,11,21,31 game someone could potentially have marked off all 4 numbers but in the 1,2,3,4 game this is not possible because no card can contain more than three of those numbers. So while the chances of getting any specific ball on the next call are always 1/(90-n) where n is the number of calls already made, some sequences of calls, although each is no more likely to happen than any other sequence of calls, have a greater propensity to result in full house faster because they do not contain groups such as 1,2,3,4 that cannot all appear on any legal bingo card. In other words, a game that starts 11,21,31,41,51,61,71,81 is more likely to have the card that does win call full house in sufficiently few calls to win the progressive jackpot (or one of the bigger prizes in a sliding jackpot game), than a game that starts 1,2,3,4,5,6,7,8. Don’t forget though that this is for EXTREMELY small values of “more likely” since the chance of winning the PJP is so tiny anyway – and any mathematical analysis is going to be somewhat flawed because it will operate on the assumption that cards are randomly generated and allocated. Since most bingo sites allow players to reject cards they don’t like the look of (and since the point of the analysis would be to decide whether there are any types of card that are best rejected), that is not going to be the case.
The number of possible sets of numbers on a legal 75 ball card is a staggering 81,324,486,324,081 if the centre square contains a number and 36,965,675,601,855 if the centre square is blank. The number of possible 75 ball cards is far greater than that (well into the septillions) as the numbers in each column can appear in any order and while two cards with different permutations of the same numbers will both achieve a coverall at the same time, this is not the case for a line or a pattern. As for the number of possible 90 ball bingo cards, it actually varies according to where you play because different bingo platforms use different rules for generating 90 ball cards! The figure of 3.6 quintillion as calculated on Stackexchange is for the version of the game as played at Virtue Fusion, where none of the columns on the card are allowed to be blank, the numbers in each column always appear in numerical order, and the distribution of numbers in the columns is slightly skewed with only 9 numbers (0-9) allowed in the first column and 11 (80-90) in the last column. At Dragonfish and Bede Gaming blank columns are allowed and the numbers do not have to appear in numerical order which results in a much larger number of possible cards; again, rearranging the order of the numbers in a column does not make any difference for full house but it does for line wins.
Card selection ideas
If maths can’t give us the answer, how about psychology? Since each game of bingo must have a winner, the chances of winning do depend on how many other cards (out of the ridiculously large number of possible cards) are actually in play. It may be possible to have a very, very slight edge over other players by selecting cards with numbers that you think are likely to be rejected by others on the grounds that if you do win, you are slightly less likely to have to share the prize pot with someone else (especially in a 90 ball game where there are three prizes).
Similarly when buying multiple cards it is slightly better to pick cards that don’t have any numbers in common with each other because while cards with numbers in common might both win, if they do you don’t get double the prize.
How many cards should you buy?
Now, is it better to buy 100 cards for one game or one card for each of 100 games? Maths CAN help us here. Let’s suppose that for each game, 1000 cards are sold. You have a 1/10 chance of being the full house winner in the first case, and a 1/1000 chance of being the full house winner for each game in the second case. To work out the odds or winning at least one of the 100 games in the second case, we first of all work out the probability of winning NONE of them – which is approximately (999/1000) to the power of 100. (Approximately, because occasionally two or more players get full house at the same time). That is 0.9048 (to 4 decimal places), making the chance of winning at least one game 0.0952, which is slightly less than 1/10. So in theory, the 100 cards for 1 game does better. But consider these points:
1) When you buy 100 cards for the same game, you set an upper limit for what you can win which is determined by the prize fund for that particular game. The upper limit for what you can win in the 100 games is the total of all prize funds which is much larger. In other words, if you win more than once in the 100 games you win more than one prize, but if you win any of the prizes more than once with the 100 cards in one game you have to split the winnings with yourself. The chance of winning more than once is very small (on the order of 1 in 10,000 to win full house twice in the example above) but the double prize makes up for the difference – especially if you play in games where there are 1TG and 2TG winners in addition to the usual.
2) Playing 100 games of bingo has vastly more entertainment value than playing 1 game of bingo (though not perhaps the most entertainment value available).
3) The mathematical analysis does not survive contact with the real world since in practice, the 100 games of bingo won’t all be the same; it’s pretty unlikely that they would all have the same number of cards sold. The smaller the total number of cards sold, the better the chance the one card has of winning (but the smaller the prize pot will be apart from in the case of a guaranteed jackpot game).
4) If you buy lots of tickets for each game, it’s really easy for spending to get out of hand.
5) In the case of a guaranteed jackpot game, it could be worth buying a lot of cards if the room seems quiet, as the prizes will be considerably bigger than they would have been if just based on the card sales (Conversely, of course, if the room seems very busy in a game with a fixed prize it may not be worth buying any cards as the prize could be worth less than it would have been if fixed by card sales).
6) It is possible to avoid the issue of competing with oneself mentioned in point 1 by buying a strip of 6 tickets for 90 ball or a strip of 3 tickets for 75 ball. In a strip, none of the numbers are repeated across multiple tickets and in fact all the possible numbers will appear once and once only (although in the 75 ball tickets three of the numbers will be obscured if there is a free centre square). Not all bingo rooms offer the opportunity to buy a strip, however; some just allocate tickets randomly.
Return To Player
But it’s not just about what the chance of winning a game of bingo is, it’s also about how much money you can expect to win overall compared to your spend on bingo tickets and here, it is important to have realistic expectations. This is called RTP (return to player) and is generally expressed as a percentage showing how much you would expect to get back overall if you played hundreds of thousands of times.
If the RTP is anything less than 100%, that is bad news for the heavy depositors we talked about at the beginning of the article – because they more they spend, the more they are likely to lose.
The RTP on online slots is generally in the region of 96%, and reputable sites such as Gala publish the RTP on each of the slots they feature so you can check before you play (in fact, UK-facing slots sites are required by law to publish the RTP, although you may have to look quite hard to find it). The RTP on the British National Lottery is described on the Camelot web site as “over 50%” so one can take a guess that it’s not very much over 50%. But what is the RTP on bingo? Hardly anywhere seems to say, with the exception of the Cozy-powered Live Bingo Network, which specified RTP in its terms and conditions and gave the RTP for bingo as 75-80%, but without explaining how that related to the huge bonuses given out by those sites. Gala Bingo used to publish the expected RTP on their bingo games (along with the expected RTP on all their slots and casino games); this could be found by following a series of less than prominent links staring with “Fairness” at the bottom of the home page. Most of their bingo games were shown as having expected RTP of 70% with some coming in at 67%. This information has since been removed (it is not known why).
One reason for all this vagueness is that RTP on bingo can’t be specified precisely ahead of time in the way that it can be on slots and instant win games:
1) Each game must have at least one winner regardless of the number of cards that have been sold.
2) Some games have guaranteed prizes so the money (or tangible prize) given out does not depend on the amount spent on tickets and this can cut both ways. A heavily publicised game with a prize of a holiday worth £5000 could easily achieve ticket sales worth a lot more than £5000 and in this case the RTP would end up being lower than usual. On the other hand, if it wasn’t well publicised and was run without an easy pre-buy arrangement at an ill thought-out time (e.g while the Strictly final was on TV) the ticket sales might fail to reach £5000 and the game would have an RTP of more than 100% (although only the actual winner would see the benefit).
3) Progressive and sliding jackpots also affect things.
However, you’d think more of the sites would publish historical or approximate expected RTP amounts, wouldn’t you, if they looked attractive for the player?
Usually it is not possible for the player to make an informed guess at the RTP of a bingo game because although they may be able to see how many players there are in the game they do not know how many cards each player has. An exception to this is the type of multi-stake bingo game that is one ticket per player.
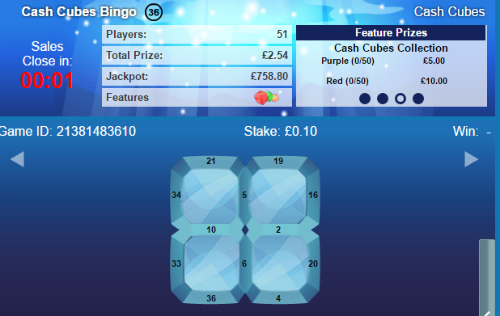
Here, we CAN make an informed guess at the RTP! There are 51 players in the room and the prize at the 10p stake level is £2.54. If all 51 players bought 10p tickets the total ticket sales would amount to £5.10 – and the £2.54 is a smidgin less than 50% of this, which is pretty dismal! In fact it is not quite as bad as it seems because this calculation does not include the progressive jackpot contribution; in the screenshot the progressive jackpot, which is split between all players if someone wins this 36 ball game in 18 or fewer calls, has grown to 7500 times the lowest stake value. Nor does it include the feature prizes which are awarded after collecting cubes over multiple games. The calculation also assumes everyone is playing with cash whereas in fact it is extremely likely that many players are playing with bonus. This game also has a guaranteed minimum prize of £2 so a similar game with fewer than 40 players would have a theoretically better RTP. Finally, the ACTUAL RTP on Cash Cubes is going to vary from game to game depending on how many tickets are sold at each stake level and what the stake level of the winning ticket is. If one player buys a 10p ticket and everyone else buys £2 tickets, but the 10p ticket wins, the player wins £2.54 from total ticket sales of £100.10. If one player buys a £2 ticket and everyone else buys 10p tickets, but the £2 ticket wins, the player wins £50.80 from total ticket sales of £7.
What IS clear from this example is that the RTP on bingo is nowhere near as good as the RTP on slots; if you think about it, the bingo site owners have to pay for the server, the chat hosts, the advertising, the promotions and so forth out of the takings and presumably they also want to make a profit, so that’s quite a large slice of the pie that is not available for RTP. Before you rush off to play slots instead of bingo though, consider this:
1) RTP of 96% on a slot does NOT mean that each and every player will get back 96% of their stake or anywhere close to that. It means that 96% of the money wagered altogether (which includes winnings as well as initial deposits) will be paid out in prizes – but when someone wins millions on a slot as happens from time to time, that comes out of the RTP, leaving a lot less for the other players.
2) You can spend (and lose) a lot of money very quickly on slots, and it’s probably going to be real money as most bingo sites won’t let you use bonuses on slots.
3) A 10p bingo ticket potentially has a great deal more entertainment value than 10p spent on a slot. Even if you can find a slot where one spin costs just 10p (and in these days of multiline slots, even if the coin size is set at 1p the minimum cost of a spin is more likely to be 20p or more), it’s over in seconds.
Finally on this topic, a word of warning. In the case of bingo games with a fixed prize that does not depend on ticket sales, the more tickets that are sold, the worse the RTP gets. It’s easy to get carried away when you see a big headline prize advertised, but when there’s a rush to buy tickets for a well publicised big money fixed jackpot game the operator may easily end up selling so many tickets that it works out as very poor value for players.
It’s all about the entertainment value
So when it comes down to it, the best attitude to have is that when you play bingo (whether online or in a bingo hall) you are paying for entertainment and while the chance that you might win big makes it extra entertaining, it is probable that you won’t win enough to cover your costs. That’s not because it’s fixed, but because the bingo site needs to cover its costs and wants to make some money, so the amount it has available for prizes is considerably less than the total paid in.
So decide how much you want to spend and stick to it, taking advantage of deposit bonuses, free bingo and penny bingo to make your money go as far as possible. Maximum entertainment value comes from striking a balance between number of cards and number of games. The more cards you play with, the more likely it is that at least one of them will do well enough to be worth watching right up until the end of the game. One strip of 6 is a good compromise – and if that pushes your budget, go for games with a lower card price.
If you are lucky enough to win big, we’d suggest taking the winnings out if and when wagering requirements permit, and playing on within your original budget. And if you don’t win – you still had a great time playing bingo and chatting, and you didn’t lose money you couldn’t afford to lose. Above all else – have fun!
At Best New Bingo Sites all of our reviews are completely honest and written by industry experts. We aim to present all our offers as transparently as possible with a full explanation of the terms and conditions. We receive commission from the sites we feature and this may affect how prominently they appear on our site and their position in our listings.






I agree bingo is rigged, and also the slots, when i play them half way through a spin i get a notice saying my internet is slow, but when playing free slots nothing happens, also when loading slots they take a long time to load when im playing with real money, but when im playing a free tournament they load really fast. When i first join sites i win sometimes big on the slots, but i think now im being monitored. Has anyone else had this issue?
Agree. Something dodgy about all the bingo sites. Especially the larger ones.
The companys will not be “in on it”! But its rigged 100%. You wont catch the people using back door methods into the wins and they will not take too much free money to draw attention from the big guns, but its EASY to see. The Chat mods have to block people who mention it, and I have no doubt the mods are clueless to it and thinks its just bad losers, but no. Ive done probability and statistics at University and I am telling you right now, its not possible its “luck”, not over an extended period of time at those rate, impossible!
Course it a fix! Your claim that those same winners buy the max tickets is nonsense when its free bingo and everyone has the same number. Explain how the same winners win multiple time every session, every day!! If you could only bet on that, because its a fact. The odds dont account for that. Maybe once in a session someone can get lucky, but this is same names multiple time per session per day. So RIGGED!
I too have witnessed a lot of the same names winning where everybody supposed have the same amount of tickets, some games have lots of players so the odds of winning are less but those same names win.
Some websites say it is a matter of luck, well I’ve seen players not or never winning but these same name ones have an awful lot of good luck to win everyday.
Some sites suppose to restrict gambling but we are told these same names spent a lot more than the average player so why are they not restricted?
i was playing recently in dond 75 room, one player was complaining that they had played all day same winners spent a fortune was going to find another site was really upset they were playing their last game and won over 700.00 pounds what do you think happened there.
It’s a game of luck
too right its fixed random number generators are not 100% random proven fact . The same names win umpteen times a day everyday on several sites i play on . Ive seen enough over past 10 years and lost thousands pounds in the process . The only way they can prove its 100% random is to have a video caller onscreen using old fashioned air and bingo ball machine . I CHALLENGE ALL SITES TO DO LIVE VIDEO SCREEN BINGO CALLING LIVE USING THIS PROVEN RANDOM PROCESS . I wont hold my breath waiting on them doing it though .
For this to be the case large numbers of people would have to be in on it at rival operators, RNG certification labs and the Gambling Commission and if there really were such a giant conspiracy an old fashioned machine via a video feed would be just as susceptible as it would have to go through the same Gambling Commission procedure to be licensed, just like live casino operators do for games like Dream Catcher and Camelot does for the lottery draw.
I have played max cards on every bingo site and ive noticed the same names winning for instance i will have 5 different sites playing at the same time and the same winner name for house will win on all 5 sites in their main rooms….these are not linked games neither to other sites…wonder how this can be as ive been watching this pattern for 10 years now 🙁
Are you sure the rooms aren’t linked? There are very few bingo rooms these days that aren’t linked across a network, but the operators often don’t make it at all clear that they are.
The Gambling Commission, who regulate all of the bingo, slot and casino sites we write about, have the following information about how to complain http://www.gamblingcommission.gov.uk/for-the-public/Your-rights/Complaints.aspx They say that complaints should initially be made to the operator and the Resolver website is one way of doing this https://www.resolver.co.uk/rights-guide/gambling
However, a complaint about the free bingo room may not even fall within their remit as since the tickets cost nothing there is no risk to the consumer. Could it be that certain players (VIPs perhaps?) are being given tickets to all the free bingo games in advance whereas regular players have to be in the room at the time to claim them?
The Gambling Commission can be contacted at [email protected] or tweet them @GamRegGB
I like playing BINGOCAMS the thing is i think there is something not right. I know you explained about big depositors buying max cards but this site has a free room and a fee paying room where you can only but a small maximum tickets , free ones you get max of 20 each but every day 24/7 the same people win . there can be 60 people playing but it’s the same 20 or so that win consistently everyday and night ,now you cannot tell me this is right or fair someone should look into this ,i would like to get in touch with the regulators as i am definitely sure there is something amiss,