Tombola Stars Game - Maths and Fairness

-
Updated: 14th Aug 2024
The Tombola Stars game is arguably one of the best daily free games ever at UK bingo sites. It combines the fun of daubing numbers yourself (something which is missing from most online bingo games) with the lure of a huge prize pot and is understandably very popular with players. But have you ever wondered about the maths behind it – and what your chances really are of winning the £30,000 prize?
- What Is Stars?
- How To Play
- The Chance Of A Win
- Missing A Day
- Possible Outcomes
- Saturday Night
- Sunday Morning
- The Big Question
- Our View
What Is Stars?
Stars is a free daily game which can be played at Tombola Bingo and at Tombola Arcade by anyone who has ever made a deposit there and has signed up to receive SMS notifications. There is a fixed prize fund of £30,000 cash each week which is split between all winners (typically one or two, sometimes as many as four). Occasionally no-one wins and in that case, the prize fund is carried over making the following week’s prize £60,000.
How To Play Stars
Each player is sent a unique 4 digit activation code via SMS on the Monday (meaning that there could be up to 10,000 players participating; if there were more, 5 digits would be required for them all to have a unique code). They can then launch the game from one of the Tombola websites or mobile apps and enter the code to activate it for the week (the code only has to be entered once to activate the game for both Tombola Bingo and Tombola Arcade).
The game card comes in the form of a scrollable, animated riverside scene with 25 stars bearing 25 of the numbers 1 – 50 and plays like a bingo game but with the winning condition of a lottery. To win, the player must match all 25 numbers in the course of the week and click on the corresponding stars to collect them. 6 numbers are called every day, so a total of 42 of the 50 numbers are called over the week. Matching 25 from 42 sounds easy, so why are there relatively few winners given the large number of players at Tombola?

The Chance Of A Win
Assuming that the cards are randomly generated and allocated, to work out the chance a particular card has of winning we need to look at all of the possible ways to choose 25 numbers out of 50 and work out what proportion of them can win given a particular set of 42 calls. There are 8 numbers out of the 50 that are NOT called during the week and a winning card will not contain any of those 8 numbers. If it contains one or more of those numbers, it loses.
Let’s consider a similar but vastly simplified case – suppose that each card contained 2 of the numbers 1 – 5, and 3 numbers were called altogether. With such small numbers, it is easy to work out the possibilities by simply listing them all. They are 1-2, 1-3, 1-4, 1-5, 2-3, 2-4, 2-5, 3-4, 3-5 and 4-5. The two things to note about this selection process is that repetitions of the same number are not allowed and order is not important – for the purposes of marking off all the numbers 1-4 is the same card as 4-1. In this type of selection process, the correct mathematical term for the results is combinations.
Now suppose that the three numbers which are called are 1, 3 and 4. The only cards that could win are the ones that do not contain either 2 or 5 – so 1-3, 1-4 and 3-4 can win and none of the others can (“can” win because the player still has to pay attention to the calls to mark off the numbers). That is 3 cards out of the 10 possibilities, so the chance of getting a potentially winning card is 3/10 or 30%.
In the first part of this calculation, we work out the number of ways to select two items from five (without repetition and with order unimportant) and in the second part we work out the number of ways to select two items from three (again without repetition and with order unimportant). But how to scale it up? To do the same calculation for Stars we need the number of combinations of 25 from 50 (all possible cards) and the number of combinations of 25 from 42 (potentially winning cards in any given week) and as you might expect these are very large numbers!
Luckily there is a mathematical formula for working the number of possible combinations out – it’s called the binomial coefficient or n choose r, where n is the total number of items and r is the number of items in the selection – and there’s even a handy calculator.
The total number of possible cards is 50 choose 25 – which is
126,410,606,437,752
(126 trillion)
The possible winning cards are a (large) subset of all possible cards – those which contain any 25 numbers out of the 42 numbers that are called during the week (and no numbers from the 8 numbers that are not called). This is 42 choose 25 – which is
254,661,927,156
(255 billion)
Divide the total number of possible winning cards by the total number of possible cards and you get 0.00201456139110765533328620909027 as the chance of getting a potentially winning card – 0.2% or approximately 1 in 500.
This is quite interesting, because
- If the cards really are randomly generated and allocated, it means that if you go on playing Stars day after day, week after week, on both Tombola Bingo and Tombola Arcade there will come a point where it becomes more likely that not that you will have received a potentially winning card in the course of your play – and that point comes after little more than three years of continuous play.
- With 1 in 500 cards a potential winner and many thousands of cards in play each week (it could be anything up to 20,000), you would expect the £30,000 to be shared by many more winners than it is.
The clue is in “day after day, week after week” – we all have busy lives and many of us are not going to remember to play every single day. So what happens if you miss a day?
Missing A Day
It turns out that while it is technically possible to win if you miss a day – or even 2 days – as it is still possible to mark off 25 numbers, it is much, much less likely.
If you play for 6 days you have to mark off 25 of 36 numbers. The total number of cards that can win is 36 choose 25 (600,805,296)and the chance of winning goes down to 0.0004% (approximately 1 in 250,000)
If you play for 5 days you have to mark off 25 of 30 numbers. The total number of cards that can win is 30 choose 25 (142,506) and the chance of winning goes down to 0.00000001% (approximately one in a billion).
No wonder you never hear of anyone winning Stars on the Friday or Saturday!
Possible Outcomes
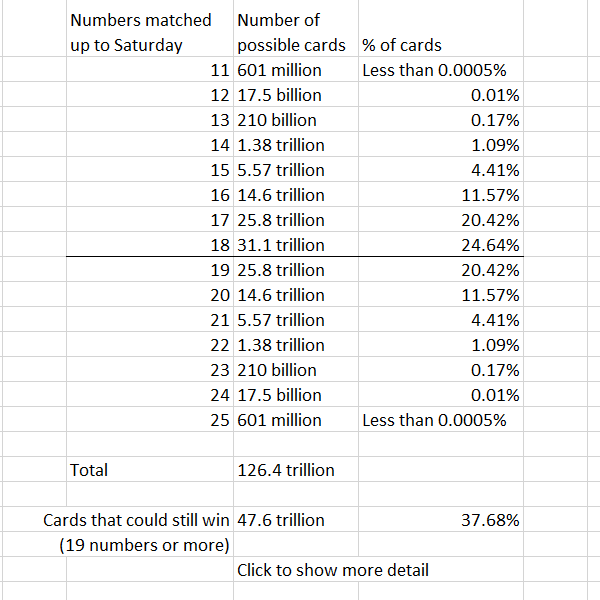
If you play every day and carry on marking your card to the end (instead of abandoning it, as most players would, if you thought there was no longer any prospect of a win) you will always match at least 17 numbers. There is 0 chance of getting 16 or fewer, because there are only 8 numbers out of the 50 that aren’t called during the week and 25 – 8 is 17. Let’s look at the case of ending on 17. In that case, all 8 of the numbers that are not called must appear on the card, together with 17 out of the 42 numbers that are called. 42 choose 17 is 254,661,927,156 – and haven’t we seen that number before? Indeed we have – it is the same as 42 choose 25 and therefore the chance of only marking off 17 numbers is just as bad as the chance of winning!
But what about getting 18 numbers? 42 choose 18 is 353,697,121,050, but we also need to look at how many combinations there are of 7 out of the 8 wrong numbers – and to find the total number of possible cards with 18 numbers matched, multiply the two together. 8 choose 7 is 8 – multiply them together and you get 2,829,576,968,400. Divide that by the total number of all possible cards to get the chance of ending on 18 calls – around 2.24%.
We can do this calculation for every possible outcome between 17 and 25.
We see the most likely outcome is 21 numbers matched – and more than 75% of cards (if marked off to the end) will end up with 20, 21 or 22 (so 3,4 or 5 Stars short of a full house).
We haven’t yet touched on the exciting part of the maths behind the game, though, which is how close you are to winning – and how likely you are actually to go on to win – when only the final day’s numbers remain to be called.
Saturday Night
You’ve played all week and marked your numbers off every day – so how likely is it that you’ll still be a contender as Sunday approaches? To have any chance of winning in the remaining 6 calls you must have marked off at least 19 numbers, but it is possible, after 6 days, to have marked off as few as 11 numbers (with all 14 numbers not yet called appearing on your card). A card with anything from 11 to 18 numbers marked off and one day left is no longer capable of winning – so how many of those cards are there? Again, this is a nice symmetrical distribution with the number of cards in the extreme case of 11 calls equal to the number of cards in the other extreme case of having won already with 25 calls, and to work out the numbers in the middle we must multiply by the number of possible combinations of numbers that haven’t yet been called.
What this means is that assuming the cards are randomly generated and allocated (but see below)
- Theoretically the most common situation to be in on Saturday is the frustrating “near miss” case of 18 numbers matched
- Only 37.68% of cards will still be in the running on Sunday morning
- More than half of those will have marked off just 19 numbers!
- As each player can play with two cards (one from each site) theoretically there is slightly more than 60% chance of having at least one card still in the running
Sunday Morning
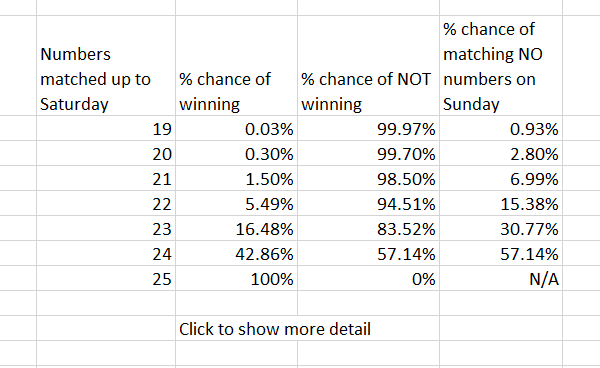
Now let’s crunch the numbers a third time, to see what the chances of going on to win from each of those positions is. Clearly a card that has already marked off 25 numbers has a 100% chance of winning (indeed, has already won), and a card that has marked off 18 or fewer has a 0 chance of winning.
Now, there are 14 numbers which haven’t yet been called – 6 which will be called on Sunday morning and 8 which won’t. The number of possible sets of 6 numbers that could be called from the 14 is 3003 (14 choose 6) and in the extreme cases of 19 and 25, it’s easy to work out how many of these are potential winners – all 3003 if 25 numbers are already marked and just 1 if all 6 numbers are still needed. We can also work out the probability distribution of the various outcomes for someone starting with 19 numbers and verify that there are 3003 possible cases and that the chance of winning with a card that starts Sunday with 19 numbers match is 1/3003 – approximately 0.033%.
But what about players who start with 20 – 24 numbers?
Here’s where it gets more complicated, because instead of being a nice symmetrical distribution the probabilities look skewed. This is because the more numbers out of the 25 you already have matched, the harder it gets to match any more. For instance, if you already have 24 numbers marked, only one of the remaining 14 numbers will be a possible match whereas if you have 19 marked, 6 out of the remaining 14 are possible matches.
Perhaps surprisingly, it turns out that regardless of how many numbers you have left to match on Sunday morning, you are more likely to match NO numbers at all from Sunday’s calls than you are to win – even if you started short of just one Star! How annoying is that!!!
The Big Question
“Assuming randomly generated and allocated cards” – but are they really? If Stars was a bingo or lottery game that cost money to play, the cards would HAVE to be randomly generated and allocated in order to meet regulatory standards – but firstly, it’s a free game with no monetary risk to the players, and secondly it may very well not even be a bingo game at all, but something else entirely. Play Stars for any length of time and you will come to believe that far from only 37.68% of cards remaining playable on Sunday morning, most or possibly even all cards do. What could be the explanation?
In order to be able to avoid allocating the 62.32% of possible cards that would not be in a potentially winning position after 6 days of play, Tombola would have to be able to identify which cards those are and that would mean that the calls for the week would have to be determined in advance, BEFORE the card allocation was done, rather than randomly generated on the fly. The rules for card generation and allocation could then be set to exclude any cards not containing 19 or more of the first 36 numbers due to be called and this would ensure that everyone who plays every day gets the full entertainment value of Sunday morning. All else being equal, it would also improve the chance of getting a potentially winning card as there would be fewer possible cards. An analogy would be a tombola where tickets ending in 0 win a prize – if you remove all the tickets ending in the digits 1-6 from the drum, you increase the chance of a randomly drawn ticket being a winner.
If the week’s calls are determined ahead of time, however, all else need not be equal as it would also be possible to include a set number of potentially winning cards; the variation in the number of winners would then be down to whether the people who get those cards actually remember to play them every day. Essentially, this would mean that the game is basically a SCRATCHCARD which is revealed in stages – rather than a bingo or lottery game.
Our View
From anecdotal evidence of the number of cards remaining playable on Sunday, it seems likely that instead of using a bingo/lottery model (randomly generated cards and randomly generated calls) Stars works on a scratchcard model (a preset series of calls and a subset of up to 20,000 cards engineered to make the game as entertaining as possible for everyone). Does this mean it could be fixed? The answer is a resounding NO for a very simple reason – the way the prize money works. Tombola give away prize money of £30,000 per week regardless of the number of winners so it is simply not possible for the game to be biased in the house’s favour.
On the contrary, Tombola Stars is almost certainly the BEST game out there in terms of fairness for players. While there are other sites including Sky Bingo and Heart Bingo which have free daily games, the prizes are small potatoes compared to the Stars prize money which amounts to well over a million pounds a year. Free daily games also usually require a minimum spend of some kind and Stars doesn’t.
Our view is that Stars is a must-play for anyone who can manage to play it without skipping any days. Where else in the online bingo world are you truly going to get something for nothing – at a minimum, the entertainment value of playing the game every day and maybe, just maybe, a big win – after all £30,000 a week has to be won by someone and with free cards, and the same number of cards for each player, everyone has an equal chance of the prize.
At Best New Bingo Sites all of our reviews are completely honest and written by industry experts. We aim to present all our offers as transparently as possible with a full explanation of the terms and conditions. We receive commission from the sites we feature and this may affect how prominently they appear on our site and their position in our listings.